Transformers for Dummies - Positional Embeddings

In the previous article of this series, we talked about how text is converted to numbers and how input embeddings are generated. There is one more layer we pass the inputs through before it is ready to be fed into Transformers’ famous Attention Layer.

Why are Positional Embeddings needed in Transformers?

LSTMs were all the rage before Transformers took over. One of the key differences between them is that LSTMs take in one word at a time.

Transformers ingest a whole sentence in one go. Thus, they don’t know which word came first.

In other words, transformers are not aware of the sequence of the words. This is a significant problem.

Let’s talk a bit about why order matters so much that we added one whole layer just to cater to it.

Take a look at the following two sentences:

Even though the flight was not delayed, she chose to go home.

Even though the flight was delayed, she chose to not go home.

Different placement of just one word, “not”, changed the meaning of the whole sentence.

Why simple approaches don’t work.

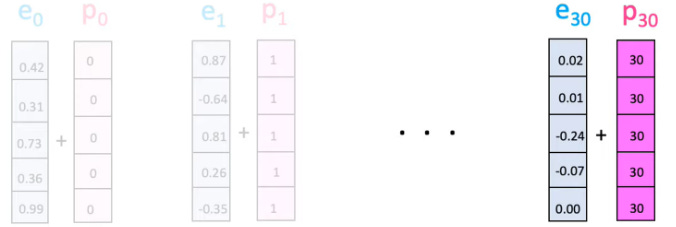
One way is to add position numbers like this:

The problem is that this may significantly distort the embeddings, especially for words at the end of huge sentences.

Okay, then why not just add fractions of the positions?

This isn’t brutally distorting the embeddings, right?

But.

For a sentence with length 50, word at position 2 will have a value 2/50. For a sentence with length 30, word at position 2 will have a value of 2/30.

It is important for the words at the same position to have the same positional embedding value otherwise it may confuse the model. It doesn’t matter what the length of the sentence is. Words at the same position should have the same positional value.

The Wave Functions

The authors of Transformer’s original paper came up with a pretty ingenious but complicated trick. They decided to use wave functions.

For those of you who remember high school physics, you’d remember that wave functions repeat after a certain period of time. sin(π) and sin(2π) have the same value. But we want the exact opposite of that, we don’t want values to repeat.

Turns out, when you change the frequency of the wave, sin(π)and sin(2π) would take on different values. Our variable i controls the frequency of the wave.

What is i in the grand scheme of Transformers? This:

To put it all together, let’s look at the following formula again:

For lower frequencies, the sin(P0) and sin(P6) are going to be quite close. But as the frequency gets higher, sin(P0) and sin(P6) are going to grow further apart and then you can tell these two words apart.

The thing is, words that are closer in meaning and context, their values are going to be close in lower dimension; they will only grow apart in a much much higher dimension. For words that are like antonyms, their values are going to look very different even in lower dimensions (see the animation below, you can see that the points have different y-axis values on the curve quite early on). Perhaps this enables embeddings to better capture nuances in similar words.

The authors of the Transformer’s paper chose to use both sine and cosine formulas. It has a very Newton’s principa mathematica’s proof’s like mathematiky reason. I’ll try to break it down as much as possible.

Say we have PE₀ and PE₆, that is, words at position 1 and 6 respectively. We want PE₆ to have a linear relationship with PE₀. Its just better for the model if the distance between two consecutive words is consistent across sentences with different lengths.

So for any offset k, PE_pos+k can be represented as a linear function of PE_pos.

Btw: AmirHossein gives an awesome deep dive into these mathematiky details in this blog.

So after all this, we finally have our position embeddings. We can now go ahead and simply add these to the word embeddings.

Our input is now ready to be fed into the next layer - The Multi-Headed Attention Layer! We’ll break that down too in the next article.

Stay tuned and my best wishes to you for the awesome product you are building with Transformers.

P.S: Feel free to point out any errors in the concepts or explanations; I'm on this learning journey myself, and your input is greatly valued.